C# 統計・微分積分・線形代数への道
目次→http://1studying.blogspot.jp/2017/08/senkei-index.html#kuw06
「関数の基礎」メモっておく。
ここでは、
「×」を「*」
「÷」や「分数」を「/」
で表現します。
「関数f(x)」とは(f(x)はxの関数)
「f(x)」は「エフエックス」と読み「関数」を指します。
「f」は「function」(関数)の略です。
「関係性のある(入力)数値と(出力)数値」の繋がり事を「関数」と呼びます。
「f(x)はxの関数」のとき「関数f(x)」は
「入力」を「x」、「出力」を「f(x)」と見立てた「関数」となります

「関数f(x)」へ入力する数値となる「変数x」を「説明変数x」と呼びます。
「関数y」とは(yはxの関数)
「入力値xの値」により、1つの「出力値yの値」が決まるとき
「yは、xの関数」
と言い、
「y=f(x)」(←入力xの値を「f(x)」が処理した結果を「y」とする)
と記述します

「関数y」として扱う「変数y」を「目的変数y」と呼びます。
「関数f(x)」と「関数y」のグラフ
「f(x)=x+2」
「y=x+2」
のような「関数の式」では必ず、
「xの数値」が決定すると「f(x)やy」が1つの数値に確定します。
(「x」の数値の確定により「f(x)やy」の数値が1つの値に確定しない場合は
「関数」とは言えません)
この「関数」の「入力値と出力値の関係性」を「グラフ」にした物が
「関数グラフ」です。
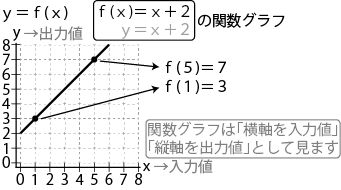
「関数の式」を「関数グラフ」にする事によって、
「入力数値」がいくつのとき「出力数値」がいくつになるかの関係性が
見た目にとてもわかりやすくなります。
「関数、関数グラフ」の注意点(方程式のグラフ)
「関数の式」とは、
「xに何か値を入れると必ずf(x)やyの値が1つに決まる」
(「x」に値が入ると「関数f(x)や関数y」が1つの値に確定する)
ような関係性の式を指します。
なので、
「関数f(x)、関数y」から出力される数値は必ず1つ
でなければいけません。
・関数式である「f(x)=x2」「y=x2」
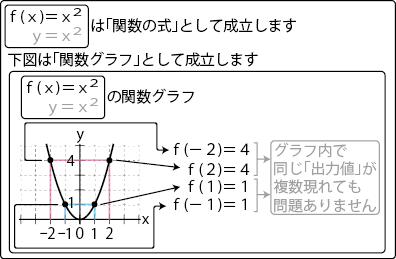
・関数式ではない「f(x)=√xまたは−√x」「y=√xまたは−√x」
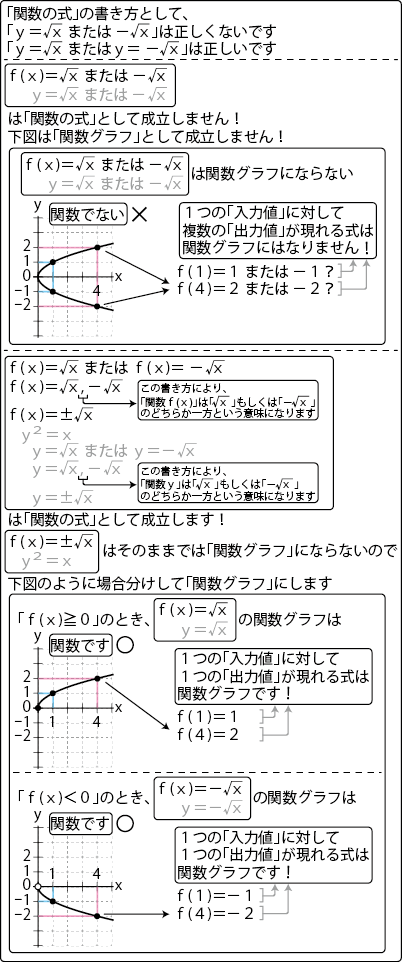
・「方程式のグラフ、円の方程式のグラフ」(陰関数)

1次式2次式3次式とは(次数と次式と元)
この後で「方程式」と「関数」についてを学ぶためには、
「n次数」と「n次式」についての理解が必要となりますので説明します。
「次式」の判断例を幾つか見てみましょう。
・「元」について…
「式」の中にある「変数の種類」の総数を「元」と言います。
「等式」と「不等式」と「恒等式」と「方程式」と「関数」の違い
「恒等式」と「方程式」と「関数」があやふやだと困るので、
ここでそれぞれの違いを軽くまとめておきます。
・「等式」とは
「=」(イコール)で結ばれた式の事です。
・「不等式」とは
「≧や≦」「>や<」「≠」(不等号)などで結ばれた式の事です。
「変数(xやyなど)」が指す「答えの範囲を解くため」に不等式を使います。
(「方程式は変数の指す値」「不等式は変数の指す範囲」を求める事が出来ます)
・「恒等式」とは(「等式」の一部)
「公式、定理、定義、法則」などと呼ばれる
「=」で結ばれた「証明する為の等式」は全て「恒等式」です。
・「方程式」とは(一次方程式 二次方程式 三次方程式)
「答えを解く為に存在する問題となる等式」つまり、
「答えを解く為の等式」の事を「方程式」と呼びます。
「方程式」では式が「1次式、2次式、3次式」かによって、
「一次方程式、二次方程式、三次方程式」と呼び方が変わります。
「方程式」は変数「xやy」などの、分からない変数の解を求める為に使う式です。
・「関数」とは(1次関数2次関数3次関数)
「関数式」は「グラフ化」した物とセットでよく扱われます。
「xに何か値を入れると必ずf(x)やyの値が1つに決まる」
ような関係性の式を「関数式」と言います。
「関数」の中で行われている計算を式として表す時、
「=の右側の式」は
「変数」に値が入った時に変換するルールとなる式
となります。
注意:
「関数」では「=の右側の式」が「1次式、2次式、3次式」かによって、
「1次関数、2次関数、3次関数」と呼び方が変わります。
「関数」は「変数」に様々な数値を入れた時の「解の値の変化」を知る為に使う式です。
1次関数2次関数3次関数のグラフ
「1次関数」「2次関数」「3次関数」の式を「グラフ」にするとそれぞれ、
「1次関数グラフ」は「直線」
「2次関数グラフ」は「放物線」
「3次関数グラフ」は「曲線」
の「グラフ」になります。
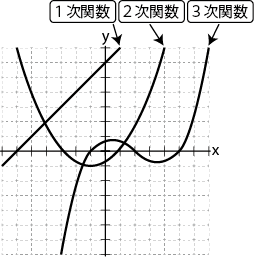
「1次関数」直線グラフ、「2次関数」放物線グラフ
については「他の章」でさらに詳しく学ぶ予定です。
C# 統計・微分積分・線形代数への道
次へ→http://1studying.blogspot.jp/2017/08/senkei-index.html#kuw07
以下のサイトを参考にしました。
【2次関数】f (x)の意味
http://kou.benesse.co.jp/nigate/math/a14m0205.html
関数f(x)[意味・使い方・読み方]
http://manapedia.jp/text/2501
恒等式と等式の違いは何ですか?
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1348651388
方程式と恒等式の違い
https://mathtrain.jp/equ_iden
【二次関数】
http://wakarimath.net/explanation/q.php?pID=E00010
3次関数はどうなる?
http://mtf.z-abc.com/?eid=829022
グラフィカルに数式を表示できる
http://www.wolframalpha.com/input/?i=y%3D-x
数学記号の表
https://ja.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6%E8%A8%98%E5%8F%B7%E3%81%AE%E8%A1%A8
数式記号の読み方・表し方
http://izumi-math.jp/sanae/report/suusiki/suusiki.htm
目次→http://1studying.blogspot.jp/2017/08/senkei-index.html#kuw06
「関数の基礎」メモっておく。
ここでは、
「×」を「*」
「÷」や「分数」を「/」
で表現します。
「関数f(x)と関数yとx」
「関数f(x)」とは(f(x)はxの関数)
「f(x)」は「エフエックス」と読み「関数」を指します。
「f」は「function」(関数)の略です。
「関係性のある(入力)数値と(出力)数値」の繋がり事を「関数」と呼びます。
「f(x)はxの関数」のとき「関数f(x)」は
「入力」を「x」、「出力」を「f(x)」と見立てた「関数」となります

「関数f(x)」へ入力する数値となる「変数x」を「説明変数x」と呼びます。
「関数y」とは(yはxの関数)
「入力値xの値」により、1つの「出力値yの値」が決まるとき
「yは、xの関数」
と言い、
「y=f(x)」(←入力xの値を「f(x)」が処理した結果を「y」とする)
と記述します

「関数y」として扱う「変数y」を「目的変数y」と呼びます。
「関数f(x)」と「関数y」のグラフ
「f(x)=x+2」
「y=x+2」
のような「関数の式」では必ず、
「xの数値」が決定すると「f(x)やy」が1つの数値に確定します。
(「x」の数値の確定により「f(x)やy」の数値が1つの値に確定しない場合は
「関数」とは言えません)
この「関数」の「入力値と出力値の関係性」を「グラフ」にした物が
「関数グラフ」です。

「関数の式」を「関数グラフ」にする事によって、
「入力数値」がいくつのとき「出力数値」がいくつになるかの関係性が
見た目にとてもわかりやすくなります。
「関数、関数グラフ」の注意点(方程式のグラフ)
「関数の式」とは、
「xに何か値を入れると必ずf(x)やyの値が1つに決まる」
(「x」に値が入ると「関数f(x)や関数y」が1つの値に確定する)
ような関係性の式を指します。
なので、
「関数f(x)、関数y」から出力される数値は必ず1つ
でなければいけません。
・関数式である「f(x)=x2」「y=x2」

・関数式ではない「f(x)=√xまたは−√x」「y=√xまたは−√x」

・「方程式のグラフ、円の方程式のグラフ」(陰関数)

1次式2次式3次式とは(次数と次式と元)
この後で「方程式」と「関数」についてを学ぶためには、
「n次数」と「n次式」についての理解が必要となりますので説明します。
式の中で
「実数」の部分を「0次数」
「変数(xやyなど)」が「単独」で使われた部分を「1次数」
「変数(xやyなど)」同士をn回「掛けた」部分を「n次数」
と表現して、
その式の中で使われる一番大きな次数の数をnとすると、
その式は「n次式」の式と言えます。
式の中で使われた最大の「次数」が
「0次数」なら「0次数」
「1次数」なら「1次式」
「2次数」なら「2次式」
「実数」の部分を「0次数」
「変数(xやyなど)」が「単独」で使われた部分を「1次数」
「変数(xやyなど)」同士をn回「掛けた」部分を「n次数」
と表現して、
その式の中で使われる一番大きな次数の数をnとすると、
その式は「n次式」の式と言えます。
式の中で使われた最大の「次数」が
「0次数」なら「0次数」
「1次数」なら「1次式」
「2次数」なら「2次式」
「次式」の判断例を幾つか見てみましょう。
「1+2*3」→「0次式」
「1」は0次数、「2*3」は0次数
この式の「最大次数は0」の為「0次式」です。
「x+1」→「1次式」
「x」は1次数、「1」は0次数
この式の「最大次数は1」の為「1次式」です。
「x2」→「2次式」
「x2」は2次式
この式の「最大次数は2」の為「2次式」です。
「x2−abc+4d3e+2」→「3次式」
「x2」は2次式、「abc」は3次式、「4d3e」は2次式、「2」は0次式
この式の「最大次数は3」の為「3次式」です。
「1」は0次数、「2*3」は0次数
この式の「最大次数は0」の為「0次式」です。
「x+1」→「1次式」
「x」は1次数、「1」は0次数
この式の「最大次数は1」の為「1次式」です。
「x2」→「2次式」
「x2」は2次式
この式の「最大次数は2」の為「2次式」です。
「x2−abc+4d3e+2」→「3次式」
「x2」は2次式、「abc」は3次式、「4d3e」は2次式、「2」は0次式
この式の「最大次数は3」の為「3次式」です。
・「元」について…
「式」の中にある「変数の種類」の総数を「元」と言います。
「6x2+4x−10」→「1元2次式」
「6x2+4y−10z」→「3元2次式」
「6xyz+2y」→「3元3次式」
「6x2y3z+2y」→「3元6次式」
後述の「方程式」の時は以下のような呼び方ができます。(この例の右辺数値は適当です)
「6x2+4x−10=0」→「1元2次方程式」
「6x2+4y−10z=1」→「3元2次方程式」
「6x3+xyz=2」→「3元3次方程式」
「6x2+4y−10z」→「3元2次式」
「6xyz+2y」→「3元3次式」
「6x2y3z+2y」→「3元6次式」
後述の「方程式」の時は以下のような呼び方ができます。(この例の右辺数値は適当です)
「6x2+4x−10=0」→「1元2次方程式」
「6x2+4y−10z=1」→「3元2次方程式」
「6x3+xyz=2」→「3元3次方程式」
「等式」と「不等式」と「恒等式」と「方程式」と「関数」の違い
「恒等式」と「方程式」と「関数」があやふやだと困るので、
ここでそれぞれの違いを軽くまとめておきます。
・「等式」とは
「=」(イコール)で結ばれた式の事です。
「(式A)=(式B)」
「2+3 = 4+1」や「a+b = c+d」など
「左の式」と「右の式」のバランスが等しい。
「=」(イコール)の事を「等号」と言います。「2+3 = 4+1」や「a+b = c+d」など
「左の式」と「右の式」のバランスが等しい。
・「不等式」とは
「≧や≦」「>や<」「≠」(不等号)などで結ばれた式の事です。
「(式A)<(式B)」
「1+2 < 3+4」や「a+b < b+d」など
「左の式」と「右の式」のバランスが等しくない(不等である)。
「≧≦><≠」の記号の事を「不等号」と言います。「1+2 < 3+4」や「a+b < b+d」など
「左の式」と「右の式」のバランスが等しくない(不等である)。
「変数(xやyなど)」が指す「答えの範囲を解くため」に不等式を使います。
(「方程式は変数の指す値」「不等式は変数の指す範囲」を求める事が出来ます)
・「恒等式」とは(「等式」の一部)
「公式、定理、定義、法則」などと呼ばれる
「=」で結ばれた「証明する為の等式」は全て「恒等式」です。
「(式A)= (式B)」
「1 = 1.0」や「x2 = x*x」や
「(x + y)2 = x2 + 2xy + y2」など
式で使われた「変数(xやyなど)」にどんな値が入っても
「左の式」と「右の式」のバランスが等しくなり式が成立する。
(「証明する為の等式」であれば、変数が式になくても良い)
「恒等式」は「等式」の中の一部です。「1 = 1.0」や「x2 = x*x」や
「(x + y)2 = x2 + 2xy + y2」など
式で使われた「変数(xやyなど)」にどんな値が入っても
「左の式」と「右の式」のバランスが等しくなり式が成立する。
(「証明する為の等式」であれば、変数が式になくても良い)
・「方程式」とは(一次方程式 二次方程式 三次方程式)
「答えを解く為に存在する問題となる等式」つまり、
「答えを解く為の等式」の事を「方程式」と呼びます。
「(式A)=(式B)」
「2x+1 = 7」や「x2+3x−4 = 0」など
「変数(xやyなど)」の「答えを解く為の等式」。
「方程式」は「等式」の中の一部です。「2x+1 = 7」や「x2+3x−4 = 0」など
「変数(xやyなど)」の「答えを解く為の等式」。
「方程式」では式が「1次式、2次式、3次式」かによって、
「一次方程式、二次方程式、三次方程式」と呼び方が変わります。
「方程式」は変数「xやy」などの、分からない変数の解を求める為に使う式です。
「一次方程式」の例(1次式)
「2x−2 = 0」は「x = 1」が答え。
「2x+1 = 7」は「x = 3」が答え。
参考→http://keisan.casio.jp/exec/system/1215392483
「二次方程式」の例(2次式)
「x2+3x−4 = 0」は因数分解(因数分解は後ほど習います)すると
「(x+4)*(x−1) = 0」となり「x=−4とx=1」が答え。
参考→http://keisan.casio.jp/exec/system/1161228770
「三次方程式」の例(3次式)
「x3−2x2−11x+12 = 0」は「x=−3とx=1とx=4」が答え。
参考→http://keisan.casio.jp/exec/system/1256966554
「方程式」では「恒等式」を使用して答えを解きます。「2x−2 = 0」は「x = 1」が答え。
「2x+1 = 7」は「x = 3」が答え。
参考→http://keisan.casio.jp/exec/system/1215392483
「二次方程式」の例(2次式)
「x2+3x−4 = 0」は因数分解(因数分解は後ほど習います)すると
「(x+4)*(x−1) = 0」となり「x=−4とx=1」が答え。
参考→http://keisan.casio.jp/exec/system/1161228770
「三次方程式」の例(3次式)
「x3−2x2−11x+12 = 0」は「x=−3とx=1とx=4」が答え。
参考→http://keisan.casio.jp/exec/system/1256966554
・「関数」とは(1次関数2次関数3次関数)
「関数式」は「グラフ化」した物とセットでよく扱われます。
「xに何か値を入れると必ずf(x)やyの値が1つに決まる」
ような関係性の式を「関数式」と言います。
「関数」の中で行われている計算を式として表す時、
「=の右側の式」は
「変数」に値が入った時に変換するルールとなる式
となります。
「(関数)=(変換ルール式)」
これに従い「関数式」
「f(x) = x+2」
「y = x+2」
のように記述できます。
この際「関数」の出力は、
「関数f(x) =x+2」では「f(1) = 3」
「関数y=x+2」では「x=1のときy=3」
のようになります。
「関数式」で使用する「=」は「等式」とは違い「変換ルール式」を指定するものです。これに従い「関数式」
「f(x) = x+2」
「y = x+2」
のように記述できます。
この際「関数」の出力は、
「関数f(x) =x+2」では「f(1) = 3」
「関数y=x+2」では「x=1のときy=3」
のようになります。
注意:
「関数」同士の「等式」や「方程式」の事を
「関数等式」や「関数方程式」と言います。
「f(x+y) = f(x)+f(y)」
のように記述します。
ここでの「=」は「等式」を意味します。
「関数式」で使用する「=」は「変換ルール式」を指定します。
違いに注意して下さい。
「関数等式」や「関数方程式」と言います。
「f(x+y) = f(x)+f(y)」
のように記述します。
ここでの「=」は「等式」を意味します。
「関数式」で使用する「=」は「変換ルール式」を指定します。
違いに注意して下さい。
「関数」では「=の右側の式」が「1次式、2次式、3次式」かによって、
「1次関数、2次関数、3次関数」と呼び方が変わります。
「関数」は「変数」に様々な数値を入れた時の「解の値の変化」を知る為に使う式です。
「1次関数」の例(1次式)
「f(x)=2x−2」
「y=2x−2」
参考→http://www.wolframalpha.com/input/?i=f(x)%3D+2x-2
「2次関数」の例(2次式)
「f(x)=x2+3x−4」
「y=x2+3x−4」
参考→http://www.wolframalpha.com/input/?i=f(x)%3Dx%5E2%2B3x-4
「3次関数」の例(3次式)
「f(x)=x3−2x2−11x+12」
「y=x3−2x2−11x+12」
参考→http://www.wolframalpha.com/input/?i=f(x)+%3D+x%5E3%E2%88%922x%5E2%E2%88%9211x%EF%BC%8B12
「f(x)=2x−2」
「y=2x−2」
参考→http://www.wolframalpha.com/input/?i=f(x)%3D+2x-2
「2次関数」の例(2次式)
「f(x)=x2+3x−4」
「y=x2+3x−4」
参考→http://www.wolframalpha.com/input/?i=f(x)%3Dx%5E2%2B3x-4
「3次関数」の例(3次式)
「f(x)=x3−2x2−11x+12」
「y=x3−2x2−11x+12」
参考→http://www.wolframalpha.com/input/?i=f(x)+%3D+x%5E3%E2%88%922x%5E2%E2%88%9211x%EF%BC%8B12
1次関数2次関数3次関数のグラフ
「1次関数」「2次関数」「3次関数」の式を「グラフ」にするとそれぞれ、
「1次関数グラフ」は「直線」
「2次関数グラフ」は「放物線」
「3次関数グラフ」は「曲線」
の「グラフ」になります。

「1次関数」直線グラフ、「2次関数」放物線グラフ
については「他の章」でさらに詳しく学ぶ予定です。
C# 統計・微分積分・線形代数への道
次へ→http://1studying.blogspot.jp/2017/08/senkei-index.html#kuw07
他
以下のサイトを参考にしました。
【2次関数】f (x)の意味
http://kou.benesse.co.jp/nigate/math/a14m0205.html
関数f(x)[意味・使い方・読み方]
http://manapedia.jp/text/2501
恒等式と等式の違いは何ですか?
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1348651388
方程式と恒等式の違い
https://mathtrain.jp/equ_iden
【二次関数】
http://wakarimath.net/explanation/q.php?pID=E00010
3次関数はどうなる?
http://mtf.z-abc.com/?eid=829022
グラフィカルに数式を表示できる
http://www.wolframalpha.com/input/?i=y%3D-x
数学記号の表
https://ja.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6%E8%A8%98%E5%8F%B7%E3%81%AE%E8%A1%A8
数式記号の読み方・表し方
http://izumi-math.jp/sanae/report/suusiki/suusiki.htm
0 件のコメント:
コメントを投稿