C# Magick.NETを使ってみる
目次→
http://1studying.blogspot.jp/2017/07/c-magicknetmokuzi.html#kuw10
「Magick.NET」でトーンカーブを適用しようとすると、
けっこう面倒くさい…
いくつかやり方があるのでメモっておく。
（コード記述内の「myMagick」はMagickImageの画像インスタンスを指します）
ガンマを使ってみる
画像にガンマを画像データへ適用する事により、
膨らんだ曲線トーンカーブならある程度、表現する事が可能です。
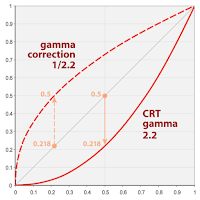
画像：Wikipedia（
https://ja.wikipedia.org/wiki/ガンマ値）より
ガンマは「1.8」と「2.2」が一般的で、
ほとんどの場合「2.2」と「1/2.2（0.45454545…）」が使用されます。
（1.4や1.5や2.5等も使う事があります。）
ガンマ「1.0」は斜めの直線となり、入出力が同じ値となる為画像の変化なし。
「1.0」から数値が離れる程、中心濃度付近の値のズレが大きくなります。
ガンマ「2.2」は「1/2.2」で相殺でき、「1.0」となります。
ガンマを使ってみる1 2 3 4 5 6 | myMagick.GammaCorrect((1 / 2.2), ImageMagick.Channels.All);
myMagick.Level(new ImageMagick.Percentage(0.0), new ImageMagick.Percentage(100.0), (2.2), ImageMagick.Channels.All);
|
めも：
ガンマのみいじる時でもレベルで処理した方が良いかも
（GammaCorrectは一時的にファイルのGamma情報も書き換えてしまう？
ファイルを保存すると正しい値に何故か戻る）
レベルを使ってみる
画像にレベルを適用する事により、
直線のトーンカーブであれば表現する事が可能です。
レベルを使ってみる1 2 | myMagick.Level(new ImageMagick.Percentage(0.0), new ImageMagick.Percentage(90.0), (1.0), ImageMagick.Channels.All);
|
これは
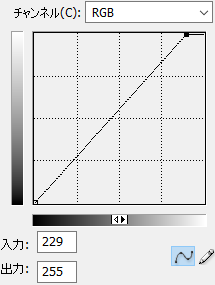
と同じ処理となります。（RGB229が90％相当）
色の反転は「0％〜100％」を「100％〜0％」にすれば可能です。
myMagick.Level(new ImageMagick.Percentage(100.0), new ImageMagick.Percentage(0.0), (1.0), ImageMagick.Channels.All);
|
のようにすれば反転します。
ガンマ処理を同時に付ける事も可能です。
ガンマ値は第３引数に入れます。
「0％～90％」の直線トーンカーブに対して
「ガンマ(1/2.2)」を適用するには次のようにします。
myMagick.Level(new ImageMagick.Percentage(0.0), new ImageMagick.Percentage(90.0), (1 / 2.2), ImageMagick.Channels.All);
|
内部では、
レベルの処理が終わった後の画像に対してガンマの処理が行われます。
「ライナーストレッチ」を使う
「ライン」と似た動作を行う「ライナーストレッチ」メソッドがあります。
この機能は「ライン」と近い機能ですが、チャンネルを指定できません。
ライナーストレッチを使う1 2 | myMagick.LinearStretch(new ImageMagick.Percentage(0.0), new ImageMagick.Percentage(100.0));
|
Fxを使ってみる
画像にFxを適用する事により、
自由曲線のトーンカーブをある程度表現する事が可能です。
但し、自由曲線を表現する為の計算式を自分で導き出してから
Fxに適用させる必要があります。
処理にも時間が掛かります。
・「gnuplot」のインストール
自由曲線を表現する為の計算式は、
「gnuplot」を使用して作ります。
その為「wgnuplo」をインストールします。
（Windows版「gnuplot」が「wgnuplo」）
http://www.gnuplot.info/
私は「gp506-win32-mingw.exe」をダウンロードして
日本語にチェックを入れる以外は、全てデフォルトでインストールしました。
「gnuplot」を起動すると
このような画面が表示されました。
・「gnuplot」で計算式を導き出す（４つのポイント用）
トーンカーブのポイントのリストを用意します。
私は以下のような物を用意しました。
「c:/testdata.txt」#これはGnuplotのファイルです。
#「c:/testdata.txt」
#トーンカーブに必要なポイントを
#行ごとに「[入力数値] [出力数値]」で
#記述してください。
#
#数値は「0.0」が「0％」、「1.0」が「100％」となります。
#
#「入力数値」と「出力数値」の間はスペースかダブで区切ります
#シャープはコメントです。
0.0 0.0
1.0 1.0
0.25 0.15
0.75 0.85
|
これをコピーしてメモ帳か何かに貼って、
「c:/testdata.txt」の名前で保存しておいて下さい。
関数を登録する為、
「gnuplot> 」へ以下のコマンドを入力します。
f(x) = a*x**3 + b*x**2 + c*x + d
|
↓
次に「C:/testdata.txt」を読み込み計算する為に、
以下のコマンドを入力します。
fit f(x) "c:/testdata.txt" via a, b, c, d
|
画面にヒープ（木構造）のテキストがバラバラと表示されます。
（処理にもの凄く時間が掛かる場合があります。）
↓
最後に「Fx」で使用できる形の計算結果を表示させる為に、
以下のコマンドを入力します。
print a,"*u^3 + ",b,"*u^2 + ",c,"*u + ",d
|
うまく行けば、以下の計算結果が表示されるはずです。
私は、
-2.13333333333333*u^3 + 3.2*u^2 + -0.0666666666666663*u + -4.85220251129635e-161
|
のように計算結果が表示されました。
この結果を後で「Fx」で使用します。
確認の為に、
計算結果のトーンカーブ図をの表示コマンドを生成します。
以下のコマンドを入力します。
print "plot [0:1][0:1] ",a,"*x**3 + ",b,"*x**2 + ",c,"*x + ",d,", 'c:/testdata.txt'"
|
これにより生成表示された以下のコマンドを入力します。
plot [0:1][0:1] -2.13333333333333*x**3 + 3.2*x**2 + -0.0666666666666663*x + -4.85220251129635e-161, 'c:/testdata.txt'
|
↓トーンカーブ図が表示されます。
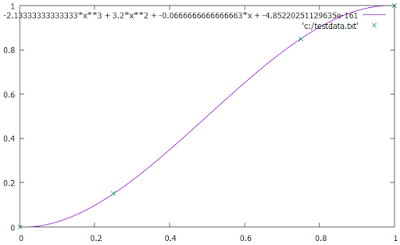Fxに計算式を適用させる
計算結果の
「-2.13333333333333*u^3 + 3.2*u^2 + -0.0666666666666663*u + -4.85220251129635e-161」
を使用して、
画像にトーンカーブ処理を行います。
1 2 3 | myMagick.Fx("-2.13333333333333*u^3 + 3.2*u^2 + -0.0666666666666663*u + -4.85220251129635e-161", ImageMagick.Channels.All);
|
Fxの処理にはかなり時間が掛かります。
これにより「Photoshop」の
0％（0）→0％（0）、
25％（64）→15％（38）、
75％（191）→85％（217）、
100％（255）→100％（256）
のトーンカーブに寄せた結果が得られます。
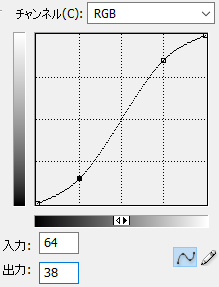
但し、
「Gnuplot」で生成した自由曲線の為、曲線が完全には一致しません。
「Photoshop」との違いはこんな感じになります。
|
０％ |
５％ |
10％ |
15％ |
20％ |
25％ |
30％ |
35％ |
40％ |
45％ |
50％ |
|
0 |
13 |
26 |
38 |
51 |
64 |
77 |
89 |
102 |
115 |
127 |
| 「Magick.NET」 |
0 |
1 |
6 |
14 |
25 |
39 |
54 |
70 |
89 |
108 |
127 |
| 「Photoshop」 |
0 |
5 |
11 |
18 |
26 |
38 |
53 |
68 |
87 |
107 |
127 |
濃度に寄ってはズレが大きくなってしまいます。
これは必ずしも「Photoshop」と同じ自由曲線にならない為です。
もっと「Photoshop」に寄せた結果が欲しい場合は、
「Gnuplot」で自由曲線を計算させる際、
細かい区切りでポイントを作り計算させればもっと数値が寄ります。
Fxで自由曲線の処理を行うと、かなり重いです。
それでも処理時間が耐えられるのであれば、使用を検討する価値はあります。
・「gnuplot」で計算式を導き出す（３ポイント用）
f(x) = a*x**2 + b*x + c
fit f(x) "c:/testdata.txt" via a, b, c
print a,"*u^2 + ",b,"*u + ",c
print "plot [0:1][0:1] ",a,"*x**2 + ",b,"*x + ",c,", 'c:/testdata.txt'"
|
f(x) = a*x**3 + b*x**2 + c*x + d
fit f(x) "c:/testdata.txt" via a, b, c, d
print a,"*u^3 + ",b,"*u^2 + ",c,"*u + ",d
print "plot [0:1][0:1] ",a,"*x**3 + ",b,"*x**2 + ",c,"*x + ",d,", 'c:/testdata.txt'"
|
f(x) = a*x**4 + b*x**3 + c*x**2 + d*x + e
fit f(x) "c:/testdata.txt" via a, b, c, d, e
print a,"*u^4 + ",b,"*u^3 + ",c,"*u^2 + ",d,"*u + ",e
print "plot [0:1][0:1] ",a,"*x**4 + ",b,"*x**3 + ",c,"*x**2 + ",d,"*x + ",e,", 'c:/testdata.txt'"
|
f(x) = a*x**5 + b*x**4 + c*x**3 + d*x**2 + e*x + f
fit f(x) "c:/testdata.txt" via a, b, c, d, e, f
print a,"*u^5 + ",b,"*u^4 + ",c,"*u^3 + ",d,"*u^2 + ",e,"*u + ",f
print "plot [0:1][0:1] ",a,"*x**5 + ",b,"*x**4 + ",c,"*x**3 + ",d,"*x**2 + ",e,"*x + ",f,", 'c:/testdata.txt'"
|
f(x) = a*x**6 + b*x**5 + c*x**4 + d*x**3 + e*x**2 + f*x + g
fit f(x) "c:/testdata.txt" via a, b, c, d, e, f, g
print a,"*u^6 + ",b,"*u^5 + ",c,"*u^4 + ",d,"*u^3 + ",e,"*u^2 + ",f,"*u + ",g
print "plot [0:1][0:1] ",a,"*x**6 + ",b,"*x**5 + ",c,"*x**4 + ",d,"*x**3 + ",e,"*x**2 + ",f,"*x + ",g,", 'c:/testdata.txt'"
|
f(x) = a*x**7 + b*x**6 + c*x**5 + d*x**4 + e*x**3 + f*x**2 + g*x + h
fit f(x) "c:/testdata.txt" via a, b, c, d, e, f, g, h
print a,"*u^7 + ",b,"*u^6 + ",c,"*u^5 + ",d,"*u^4 + ",e,"*u^3 + ",f,"*u^2 + ",g,"*u + ",h
print "plot [0:1][0:1] ",a,"*x**7 + ",b,"*x**6 + ",c,"*x**5 + ",d,"*x**4 + ",e,"*x**3 + ",f,"*x**2 + ",g,"*x + ",h,", 'c:/testdata.txt'"
|
f(x) = a*x**8 + b*x**7 + c*x**6 + d*x**5 + e*x**4 + f*x**3 + g*x**2 + h*x + i
fit f(x) "c:/testdata.txt" via a, b, c, d, e, f, g, h, i
print a,"*u^8 + ",b,"*u^7 + ",c,"*u^6 + ",d,"*u^5 + ",e,"*u^4 + ",f,"*u^3 + ",g,"*u^2 + ",h,"*u + ",i
print "plot [0:1][0:1] ",a,"*x**8 + ",b,"*x**7 + ",c,"*x**6 + ",d,"*x**5 + ",e,"*x**4 + ",f,"*x**3 + ",g,"*x**2 + ",h,"*x + ",i,", 'c:/testdata.txt'"
|
f(x) = a*x**9 + b*x**8 + c*x**7 + d*x**6 + e*x**5 + f*x**4 + g*x**3 + h*x**2 + i*x + j
fit f(x) "c:/testdata.txt" via a, b, c, d, e, f, g, h, i, j
print a,"*u^9 + ",b,"*u^8 + ",c,"*u^7 + ",d,"*u^6 + ",e,"*u^5 + ",f,"*u^4 + ",g,"*u^3 + ",h,"*u^2 + ",i,"*u + ",j
print "plot [0:1][0:1] ",a,"*x**9 + ",b,"*x**8 + ",c,"*x**7 + ",d,"*x**6 + ",e,"*x**5 + ",f,"*x**4 + ",g,"*x**3 + ",h,"*x**2 + ",i,"*x + ",j,", 'c:/testdata.txt'"
|
f(x) = a*x**10 + b*x**9 + c*x**8 + d*x**7 + e*x**6 + f*x**5 + g*x**4 + h*x**3 + i*x**2 + j*x + k
fit f(x) "c:/testdata.txt" via a, b, c, d, e, f, g, h, i, j, k
print a,"*u^10 + ",b,"*u^9 + ",c,"*u^8 + ",d,"*u^7 + ",e,"*u^6 + ",f,"*u^5 + ",g,"*u^4 + ",h,"*u^3 + ",i,"*u^2 + ",j,"*u + ",k
print "plot [0:1][0:1] ",a,"*x**10 + ",b,"*x**9 + ",c,"*x**8 + ",d,"*x**7 + ",e,"*x**6 + ",f,"*x**5 + ",g,"*x**4 + ",h,"*x**3 + ",i,"*x**2 + ",j,"*x + ",k,", 'c:/testdata.txt'"
|
f(x) = a*x**11 + b*x**10 + c*x**9 + d*x**8 + e*x**7 + f*x**6 + g*x**5 + h*x**4 + i*x**3 + j*x**2 + k*x + l
fit f(x) "c:/testdata.txt" via a, b, c, d, e, f, g, h, i, j, k, l
print a,"*u^11 + ",b,"*u^10 + ",c,"*u^9 + ",d,"*u^8 + ",e,"*u^7 + ",f,"*u^6 + ",g,"*u^5 + ",h,"*u^4 + ",i,"*u^3 + ",j,"*u^2 + ",k,"*u + ",l
print "plot [0:1][0:1] ",a,"*x**11 + ",b,"*x**10 + ",c,"*x**9 + ",d,"*x**8 + ",e,"*x**7 + ",f,"*x**6 + ",g,"*x**5 + ",h,"*x**4 + ",i,"*x**3 + ",j,"*x**2 + ",k,"*x + ",l,", 'c:/testdata.txt'"
|
めも：
・plotのsmoothオプションで
「plot [0:1][0:1] "c:/testdata.txt" smooth csplines, "c:/testdata.txt"」
と入力するとグラフのみ表示出来る、計算式への変換は出来ないっぽいので諦めた。
・IM使用例→
http://www.imagemagick.org/Usage/color_mods/#curves
計算式を導き出すシェルスクリプトがある。使えそう？
・fxだと処理が重いのが解決できないか？
→256階調全ての変換テーブル作ってしまい、
Pixel毎の数値を調べてテーブルに従って自前で変換すれば、fxより高速化できる？
（「Q16」で65535の場合どうする？）
→下記「FunctionのPolynomialを使ってみる」で解決。
modulateを使ってみる
「モデュレート」はトーンカーブと言うよりかは、
「明度、彩度、色相」を操作する機能です。
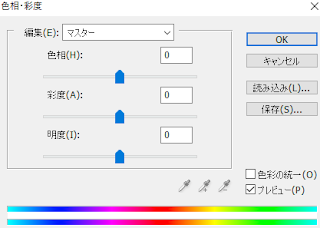
以下のように記述します。
モデュレートで明度、彩度、色相変更1 2 | myMagick.Modulate(new ImageMagick.Percentage(100.0), new ImageMagick.Percentage(100.0), new ImageMagick.Percentage(100.0));
|
入力数値の違いによる結果の違いは、
以下のサイトを参考にすると良いと思います。
「imagemagick 画像加工２（-modulate -contrast）」
http://marunouchi-tech.i-studio.co.jp/1661/
SigmoidalContrastを使ってみる
「シグモイダルコントラスト」を使うと、
濃度0%と100％を固定したざっくりしたトーンカーブを表現する事ができます。
Sigmoidalは「Ｓ字形状」という意味です。
本来「シグモイダルコントラスト」は、
「Ｓ字カーブ」のトーンカーブで画像変換する機能なのですが、
「Ｓ字カーブ」の中心ポイントを濃度0％や100％にコントロールする事により、
膨らんだトーンカーブとＳ字のトーンカーブをある程度表現できます。
引数の説明
第１引数（シャープ）：コントラストをどうするか。
trueはコントラストを上げる、falseはコントラストを下げる。
（trueはトーンカーブがＳ字、falseはトーンカーブが逆Ｓ字となる。）
通常はtrueを選んで下さい。
第2引数（コントラスト）：Ｓ字のカーブを強くします。
0意味無し、1で弱め、3で一般的、5で強め、20で極端に掛かります
第3引数（中間点）：Ｓ字の中心ポイント
（RGBの場合0％白、50％グレー、100％黒）
50％で普通に「Ｓ字カーブ」を描きます。
0％で盛り上がるように膨らんだカーブを描きます。（中心が濃くなる）
100％で掘り下げたように窪んだカーブを描きます。（中心が薄くなる）
（注意：第1引数をfalseにした場合、結果が逆になります。）
「シグモイダルコントラスト」の使用
様々な「シグモイダルコントラスト」を利用してみます
「Ｓ字カーブ」は中心ポイントを動かせば様々な「Ｓ字カーブ」を表現できます。
「膨らんだカーブ」と「窪んだカーブ」はカーブ曲線がガンマに似ています。
「シグモイダルコントラスト」の利用1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | double set1_100 = 50.0;
myMagick.SigmoidalContrast(true, (set1_100 * 0.05), new ImageMagick.Percentage(50.0));
double set1_100 = 50.0;
myMagick.SigmoidalContrast(false, (set1_100 * 0.05), new ImageMagick.Percentage(50.0));
double set1_100 = 50.0;
myMagick.SigmoidalContrast(true, (set1_100 * 0.1), new ImageMagick.Percentage(0.0));
double set1_100 = 50.0;
myMagick.SigmoidalContrast(false, (set1_100 * 0.1), new ImageMagick.Percentage(100.0));
double set1_100 = 50.0;
myMagick.SigmoidalContrast(false, (set1_100 * 0.1), new ImageMagick.Percentage(0.0));
double set1_100 = 50.0;
myMagick.SigmoidalContrast(true, (set1_100 * 0.1), new ImageMagick.Percentage(100.0));
|
「シグモイダルコントラスト」は
「ImageMagick」で使用するとチャンネルを指定ができるのですが、
「Magick.NET」だとチャンネルが指定出来ません。
バージョンアップで修正されるとよいのですが…。
（他に何か良い方法があれば教えて下さい。）
FunctionのPolynomialを使ってみる
FunctionのPolynomialを使うと、Fxより早い処理速度で
自由曲線のトーンカーブをある程度表現する事が可能です。
IM使用例→
http://www.imagemagick.org/Usage/transform/#function_polynomial
FunctionのPolynomial1 2 3 4 5 6 7 8 9 | double[] param = new double[]
{
-2.13333333333333,
3.2, -0.0666666666666663,
-4.85220251129635e-161
};
myMagick.Evaluate(ImageMagick.Channels.Gray, ImageMagick.EvaluateFunction.Polynomial, param);
|
パラメータの数値は上記「Fxをつかってみる」で生成した数値を参考にします。
他
以下のサイトを参考にしました。
stackoverflow
https://stackoverflow.com/questions/27468172/control-points-to-curve-formula-for-imagemagicks-fx-function-using-gnuplot-o
「gnuplot」の初歩
http://graph.pc-physics.com/
Fxについての説明
https://www.imagemagick.org/script/fx.php
「Gnuplot」でfitさせる為のFX関数
http://www.imagemagick.org/Usage/color_mods/#curves
gnuplotで多変数関数のフィットをするには？
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11110099541
人力検索はてな、画像を明るく（あるいは暗く）するには
http://q.hatena.ne.jp/1288094046
