C# 統計･微分積分･線形代数への道
目次→http://1studying.blogspot.jp/2017/08/senkei-index.html#kuw02
「正弦定理、余弦定理」について説明、メモ
「正弦定理、余弦定理」が成り立つ事が感覚的に分かるように、
出来るだけ図を使い「正弦定理、余弦定理」が成り立つ事を確認してみます。
ここでは、
「×」を「＊」
「÷」や「分数」を「／」
で表現します。
説明にあたって以下の呼び方をする事があります。
sinA＝sinθ＝正弦＝対辺の比率←このサイトでは「対辺率」とも呼びます
cosA＝cosθ＝余弦＝底辺の比率←このサイトでは「底辺率」とも呼びます
tanA＝tanθ＝正接＝斜辺の傾き←このサイトでは「傾き」とも呼びます
文字辞書変換
「△」は「サンカク」で変換
「∠」は「カク」で変換出来ます。
三角形「△」
「△」は三つの辺で成り立つ「三角形」を表します。
「△ABC」と書いた場合、
「∠A∠B∠C」で構成された三角形を指します。
角「∠」
「∠」は「角」を表す物です。
「∠A」はAの角そのものです。
厳密には角度を表す場合の「∠Aの角度」とは区別されますが、
「∠A = 00°」という書き方が普通に使われます。
「なす角」
「∠A」を「∠BAC」と書く事もあります。
（「∠BAC」の真ん中の文字の「∠A」を指す。）
この時、「∠A」の角度の事を
「辺ABと辺ACのなす角」や「辺c辺bのなす角」
といった言い方をします。
「外接円」「内接円」
「△ABCの外接円」と書いた場合、
「∠A∠B∠C」に接点のある「正円」の事を指します。
「△ABCの内接円」と書いた場合、
「三角形の３辺」に接する「正円」の事を指します。
声に出す時は…
「a」は「辺a」ヘンエー
「∠A」は「角A」カクエー
と、「辺」と「角」で区別した方が認識ズレを防げます。
「正弦」と「余弦」
「正弦定理」と「余弦定理」は
三角形の「辺」や「角度」を計算する事の出来る「定理」です。
「正弦定理」では「外接円」の「半径」も求める事が出来ます。
「正弦」は「sin」、「余弦」は「cos」の事を指します。
その為、
「正弦定理」は「sinの定理」（対辺の比率sinを使った公式）、
「余弦定理」は「cosの定理」（底辺の比率cosを使った公式）、
と言われています。
「正弦定理」と「余弦定理」で求める
「三角形」の辺や角度を求める際、
「正弦定理」を使うと、
「１つの辺の長さ」と「２つの角度」から他の「２つの辺の長さ」求める
「２つの辺の長さ」と「１つの角度」から他の「１つの角度」求める
「一つの辺」とそれと向かい合った「１つの角度」から「外接円の半径Ｒ」を求める
のようにして、「三角形」の各値を求める事が出来ます。
おおよそですが、
「得られる角や辺の値の数」と「求めたい角度か辺の値１つ」を合わせた時の総数が
「２辺２角」であれば「正弦定理」を使うと良いです。
つまり、
求める角度、辺を含め「２辺２角」の時は「正弦定理」
「余弦定理」を使うと
「２つの辺の長さ」と「１つの角度」から他の「１つの辺の長さ」を求める
「３つの辺の長さ」から「３つの角度」を求める
のようにして、「三角形」の各値を求める事が出来ます。
おおよそですが、
「得られる角や辺の値の数」と「求めたい角度か辺の値１つ」を合わせた時の総数が
「３辺１角」であれば「余弦定理」を使うと良いです。
つまり、
求める角度、辺を含め「３辺１角」の時は「余弦定理」
極端な話、
「三角形」でさえあれば「正弦定理」か「余弦定理」を使う事で、
・「三角形」の「１つの辺の長さ」が知りたい場合は
他の「１つの辺の長さ」と「２つの角度」
か
他の「２つの辺の長さ」と「１つの角度」
のどちらかの情報が分かれば求める事が可能。
・「三角形」の「１つの角度」が知りたい場合
他の「２つの角度」
か
「３つの辺」
のどちらかの情報が分かれば求める事が可能。
ってだけの事です。
「C# 数学１」で
「直角三角形」のときに使用出来る「辺の比率」や「内角」を求める事が出来る
「三角比」を学びました。
「正弦定理」と「余弦定理」は「(直角でない)三角形」に対しても
「各辺の値」や「内角」を求める事が出来ます。
この後に学ぶ「正弦定理」「余弦定理」の証明の流れを見れば、
結局、「直角三角形の三角比」の定理を使い
「正弦定理」「余弦定理」が成り立っている事が分かると思います。
「正弦定理」を使った計算の方法
「△ABC」があり、
「BC間を辺a」「AC間を辺b」「AB間を辺c」として、
「外接円」の半径を「R」とする。
このとき、
「∠Aの対辺が辺a」
「∠Bの対辺が辺b」
「∠Cの対辺が辺c」
となります。
この時、以下の定理が成り立ちます。
この式を変形すれば、
「１つの辺の長さ」と「２つの角度」から
他の「２つの辺の長さ」を求める事が出来ます。
「正弦定理」を使い、
「辺a」を求める形に式を変形してみます。
この、
「正弦定理」の式を変形した『「辺Ａ」を求める式』から
『各「辺の値」を求める式』を作ると以下の形にまとめる事が出来ます。
「正弦定理」の式を使い、
「sin∠Ａ」を求める形に式を変形してみます。
そこから更に「逆三角関数」を使い、
直接「∠Ａ」を求められるか試してみます。
この、
「正弦定理」の式を変形した『「sin∠Ａ」を求める式』から
『各「sinの角度」を求める式』を作ると以下の形にまとめる事が出来ます。
この「sinの角度」を求める式の形は非常によく使われる為、
「正弦定理」とセットでよく覚えられています。
また、
以下のように式を変形すると
「三角形の外接円の半径Ｒ」を計算する事ができます。
「余弦定理」を使った計算の方法
「余弦定理」には「第一余弦定理」と「第二余弦定理」があります。
「第一余弦定理」は
のような式となりますが、
「第一余弦定理」は現在あまり使われていません。
その為、
最近では「余弦定理」と言った時には暗黙的に
「第二余弦定理」の事を指します。
「第二余弦定理」は
「２つの辺の長さ」と「１つの角度」から
他の「１つの辺の長さ」を求める事が出来ます。
式を変形すれば、
「３つの辺の長さ」から「３つの角度」を求める事が出来ます。
「第二余弦定理」を元に「cos角度」を求める形に式を変形すると以下のようになります。
よって、以下のような式の形となります。
この形は非常によく使われる為、
「第二余弦定理」とセットでよく覚えられているようです。
『「第二余弦定理」の式変形後』の「sin∠Ａ」を求める式から、
「逆三角関数」を使い、直接「∠Ａ」を求められるか試してみます。
「逆三角関数」を使えば「cos∠Ａ」から「∠Ａ」を求める事が可能です。
ここでは実際に例題を作り、
「正弦定理」と「余弦定理」を使って問題を解いてみます。
「鈍角」「直角」「鋭角」
「三角形」の「１つの角度」は必ず「０°〜180°の間の角度」となります。
「１つの角度」は大きさの範囲により以下のような名前が付けられています。
「正弦定理」「余弦定理」どちらを使うかの判断
この後出てくる例題の「三角形」の「角度」や「辺」を実際に求めるとき、
「正弦定理」と「余弦定理」のどちらを使うか
の判断は概ね以下を基準にして決める事になります。
「正弦定理」を使い求めた「sinθ」の値を「角度θ」に変換する時です。
「三角形」の「１つの角度の範囲」は「０°〜180°の範囲内の角度」となります。
これを前提として「sinθ」の値を「角度θ」に変換する際、
「sinθ、角度θ」が「直角」で無い時、
(「sinθ」の値が「１」以外の時、「角度θ」の値が「90°」以外の時)
「角度θ」の値は
「鈍角の角度」と「鋭角の角度」の「２つの角度」を指します。
「２つの角度」のうちどちらの角度かに絞り込みたい場合は、
他の与えられた情報を元に「１つの角度」へと絞り込む
「解の吟味」と言われる工程が必要です。
このような注意が必要なのは、
「正弦定理」で「sinθ」から「角度」を求める
時だけです。
「正弦定理」で「辺」を求める
「余弦定理」で「辺」や「角度」を求める
場合は求めた値がそのまま答えとなります。
(「辺」の値を求めた時の答えは必ず「＋の値」となります)
「cosθ」から「角度」を求めた場合は問題無し。
「例題の準備」
それではまず、例題の為の三角形を準備をします。
ここではこの三角形を使い例題を作り、
各「辺」や各「角度」の答えを求めてみます。
「例題１」(角度を求める)
「∠Ｂ」を求めよ
「２辺２角」なので「正弦定理」を利用して「∠Ｂ」を求めてみます。
「正弦定理」で「sinθ」を求めると「１つの値」となります。
「sinθ」から「角度θ」を求めると殆どの場合「２つの角度の値」となります。
「２つの角度の値」から「１つの角度の値」に絞り込みたい場合は、
他から得られる情報を駆使して「解の吟味」をする必要があります。
(もちろん常に「解の吟味」が可能とは限りませんので、
解が絞り込めない場合は解が複数になる事もあります)
「例題２」(角度を求める)
「∠Ｂ」を求めよ
「３辺１角」なので「余弦定理」を利用して「∠Ｂ」を求めてみます。
「余弦定理」で「cosθ」を求めると「１つの値」となります。
「cosθ」から「角度θ」を求めると「１つの値」となります。
「例題３」(sinＡとcosＡの相互変換)
「三角形」の
「sinＡ」から「cosＡ」を求めたとき
「cosＡ」から「sinＡ」を求めたとき
の違いを以下の例題で確認しておいて下さい。
「例題４」(辺を求める)
「辺ｃ」を求めよ
「２辺２角」なので「正弦定理」を利用して「辺ｃ」を求めてみます。
「sin(105°)」を「加法定理」で求める
「sin(105°)」は「sin(60°＋45°)」のように
「計算しやすい角度同士の足し算」で表す事ができます。
これを「加法定理」と言う定理を使い計算すると以下のようになります。
これにより、「sin(105°)」の値を求める事が出来ました。
「三角関数」の中途半端な角度を手作業で求めたい時は、
「加法定理、倍角公式、3倍角公式、半角公式」
などを駆使して値を求める事になります。
ここでは詳しく学びませんが、
「加法定理」の「sin(α＋β)」「sin(α−β)」「cos(α＋β)」「cos(α−β)」
の計算方法位は覚えておいても損は無いです。
但しこれらはあくまで「手計算」で計算を行う際に使用する方法です。
当たり前の事ですが、
結局は「関数電卓」で「三角関数」の角度を求めるのが一番手っ取り早くて簡単です。
ここから先は、
「正弦定理」と「余弦定理」の証明を
出来るだけ図を使い説明してみます。
「正弦定理」の証明を学ぶ前に
「円周角の定理」と「外角の定理」と「四角形の外接円」について知る必要があります。
「円周角」と「中心角」とは
「円周角」と「中心角」とは以下の部分の事を指します
「円周角の定理」
「円周角」と「中心角」は常に以下のような関係にあります。
このため、
「直径」の線を辺として三角形を作ると、
必ず「円周角」が「90°」の「直角三角形」となります。
「円周角の定理」の証明(外角の定理)
「円周角の定理」の証明を行います。
まずは三角形の「外角の定理」を知っておく必要があります。
・三角形の「外角の定理」
それでは、
「円周角の定理」の証明を行います。
・「円周角の定理」の証明、その１
・「円周角の定理」の証明、その２
・「円周角の定理」の証明、その３
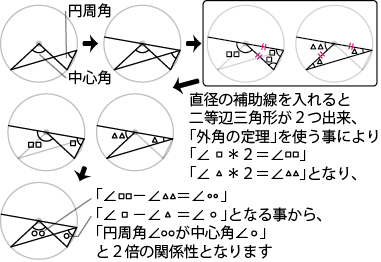
・「円周角の定理」の証明、その４
正円上の「円周角と中心角」の全ての場合分けとなる
上記『「円周角の定理」の証明、その１〜３』により
常に「円周角の２倍が中心角」と言えます。
つまり、
正円の
「中心角」が１つの角度であるとき、
「円周角」の角度はどの位置にあっても常に「同じ角度」を保つ
ことが分かります。
「円周角の定理の逆」
この「円周角の定理の逆」を使用すれば、
以下のようにして四角形の各角度を求める事が出できます。
「四角形の外接円」
「四角形の外接円の性質」の証明は以下の通りです。
三角形の角度の種類（鋭角、直角、鈍角）
三角形の角度には「鋭角、直角、鈍角」の３種類が存在します。
「∠Ａ」の角度が「鋭角」か「直角」か「鈍角」かによって、
「正弦定理」の証明方法が変わります。
「正弦定理」の覚え方
・「正弦定理」を覚える
上記公式の角度と辺の関係は以下のイメージで覚えておくと良さそうです。
・「辺」を求める形を覚える（正弦定理）
「正弦定理」の公式から「辺ａ」を知る為に、
「辺ａの値」を求める式に変形すると以下の式となります。
（式の変形方法は前述『「正弦定理」計算方法』に記述してあります）
この『「正弦定理」の式変形後』の式は無理に覚える必要はなく、
毎回「正弦定理」の公式から式を変形して導き出した方が早いです。
一応この式をイメージで表すと以下のような感じになります。
・「角度」を求める形を覚える（正弦定理）
「正弦定理」の公式から「sin∠Ａ」を知る為に、
「sinの角度」を求める式に変形すると以下の式となります。
（式の変形方法は前述『「正弦定理」計算方法』に記述してあります）
この『「正弦定理」の式変形後』の式は無理に覚える必要はなく、
毎回「正弦定理」の公式から式を変形して導き出した方が早いです。
一応この式をイメージで表すと以下のような感じになります。
「正弦定理」は「sin」を使用した定理の事です。
（対辺の比率sinを使用した定理。「正弦」の事を「sin」と呼びます）
それでは、
「正弦定理」の証明を
「鋭角」「直角」「鈍角」それぞれの状況で行います。
「鋭角(∠Ａ＜90°)」三角形の「正弦定理」の証明
「正弦定理」の公式と同じ式となる事が分かります。
「直角(∠Ａ＝90°)」三角形の「正弦定理」の証明
「正弦定理」の公式と同じ式となる事が分かります。
「鈍角(∠Ａ＞90°)」三角形の「正弦定理」の証明
「正弦定理」の公式と同じ式となる事が分かります。
これから行う「余弦定理の証明」に必要となる知識を
ざっと羅列しておきます。
「三角比の各辺の値の求め方」「180°−θ公式」
これは、前回「C# 数学１」で学んだ内容ですね、
（「三角比の角辺の値の求め方」は「正弦定理の証明」でも出てきました）
「余弦定理」の証明では、以下のような形で頻繁に使用されますので、
しっかりと覚えておいて下さい。
「(三平方)ピタゴラスの定理」
これも、前回「C# 数学１」で学んだ内容ですね
「三角関数」の公式２
これも、前回「C# 数学１」で学んだ内容です。
「sinθ」か「cosθ」のどちらかの値が分かれば
もう一つの値も分かるという公式です。
三角形の角度の種類（鋭角、直角、鈍角）
三角形の角度には「鋭角、直角、鈍角」の３種類が存在します。
「∠Ａ」の角度が「鋭角」か「直角」か「鈍角」かによって、
「第二余弦定理」の証明方法が変わります。
「第二余弦定理」の覚え方
・「第二余弦定理」を覚える
上記公式の式は以下のイメージで覚えておくと良さそうです。
「辺ａ」以外の「辺ｂ」「辺ｃ」を求める式でも
同じ手順で式を作る事ができます。
・「角度」を求める形を覚える（余弦定理）
「第二余弦定理」の公式から「cos∠Ａ」などの
「cosの角度」を求める形に式を変形すると以下ような式となります。
（式の変形方法は前述『「余弦定理」計算方法』に記述してあります）
上記全ての辺から角度を求める式は以下のイメージで覚えておくと良さそうです。
「cos∠Ａ」以外の「cos∠Ｂ」「cos∠Ｃ」を求める式でも
同じ手順で式を作る事ができます。
「余弦定理」は「cos」を使用した定理の事です。
（底辺の比率cosを使用した定理。「余弦」の事を「cos」と呼びます）
それでは、
「第二余弦定理」の証明を
「鋭角」「直角」「鈍角」それぞれの状況で行います。
「鋭角(∠Ａ＜90°)」三角形の「第二余弦定理」の証明
「余弦定理」の公式と同じ式となる事が分かります。
では、以下のような「鋭角」の三角形の時はどう証明すれば良いのでしょうか？
これは、以下のように考えれば解決できます。
これで証明できるのですが、
もう少し向き合った証明の仕方も試してみます。
「余弦定理」の公式と同じ式となる事が分かります。
「直角(∠Ａ＝90°)」三角形の「第二余弦定理」の証明
「余弦定理」の公式と同じ式となる事がわかります。
「鈍角(∠Ａ＞90°)」三角形の「余弦定理」の証明
「余弦定理」の公式と同じ式となることが分かります。
証明の為の三角形の形２パターン
三角形の「底辺」に対して「頂点∠Ａ」がどの位置にあるかによって
「第一余弦定理」の証明方法が変わります。
「第一余弦定理」のおさらい
通常「余弦定理」と言った場合「第二余弦定理」の事を指します。
「第一余弦定理」の方の定理は使われる事が少ないです。
「頂点が底辺の範囲内」のときの「第一余弦定理」の証明
「第一余弦定理」の公式と同じ式となる事が分かります。
「頂点が底辺の範囲外」のときの「第一余弦定理」の証明
「第一余弦定理」の公式と同じ式となる事が分かります。
「正弦定理」と「外接円の半径を求める形」
「正弦定理」の式変形（辺を求める形）
「正弦定理」の式変形（sin角度を求める形）
「第一余弦定理」(あまり使われません)
「第二余弦定理」（辺を求める）
「第二余弦定理」の式変形（cos角度を求める形）
C# 統計･微分積分･線形代数への道
次へ→http://1studying.blogspot.jp/2017/08/senkei-index.html#kuw03
以下のサイトを参考にしました。
正弦定理とは何か？2つの視点から分かる公式の覚え方・考え方
http://atarimae.biz/archives/18398
正弦定理を使った練習問題一覧
http://manapedia.jp/text/2916?page=3
正弦定理と余弦定理の違いと使い方
http://www24.atpages.jp/venvenkazuya/mathA/Agraphic6.php
正弦定理とは？公式や余弦定理との使い分けをわかりやすく解説！
https://www.studyplus.jp/353
【図形と計量】正弦定理と余弦定理のどっちを使えばいいんですか？
https://kou.benesse.co.jp/nigate/math/a13m0316.html
5分でわかる！正弦定理と余弦定理の使い分け
https://www.try-it.jp/chapters-6150/sections-6229/lessons-6250/
目次→http://1studying.blogspot.jp/2017/08/senkei-index.html#kuw02
「正弦定理、余弦定理」について説明、メモ
「正弦定理、余弦定理」が成り立つ事が感覚的に分かるように、
出来るだけ図を使い「正弦定理、余弦定理」が成り立つ事を確認してみます。
ここでは、
「×」を「＊」
「÷」や「分数」を「／」
で表現します。
説明にあたって以下の呼び方をする事があります。
sinA＝sinθ＝正弦＝対辺の比率←このサイトでは「対辺率」とも呼びます
cosA＝cosθ＝余弦＝底辺の比率←このサイトでは「底辺率」とも呼びます
tanA＝tanθ＝正接＝斜辺の傾き←このサイトでは「傾き」とも呼びます
「△」「∠」「なす角」「外接円」について
文字辞書変換
「△」は「サンカク」で変換
「∠」は「カク」で変換出来ます。
三角形「△」
「△」は三つの辺で成り立つ「三角形」を表します。
「△ABC」と書いた場合、
「∠A∠B∠C」で構成された三角形を指します。
角「∠」
「∠」は「角」を表す物です。
「∠A」はAの角そのものです。
厳密には角度を表す場合の「∠Aの角度」とは区別されますが、
「∠A = 00°」という書き方が普通に使われます。
「なす角」
「∠A」を「∠BAC」と書く事もあります。
（「∠BAC」の真ん中の文字の「∠A」を指す。）
この時、「∠A」の角度の事を
「辺ABと辺ACのなす角」や「辺c辺bのなす角」
といった言い方をします。
「外接円」「内接円」
「△ABCの外接円」と書いた場合、
「∠A∠B∠C」に接点のある「正円」の事を指します。
「△ABCの内接円」と書いた場合、
「三角形の３辺」に接する「正円」の事を指します。
声に出す時は…
「a」は「辺a」ヘンエー
「∠A」は「角A」カクエー
と、「辺」と「角」で区別した方が認識ズレを防げます。
「正弦定理」と「余弦定理」とは
「正弦」と「余弦」
「正弦定理」と「余弦定理」は
三角形の「辺」や「角度」を計算する事の出来る「定理」です。
「正弦定理」では「外接円」の「半径」も求める事が出来ます。
「正弦」は「sin」、「余弦」は「cos」の事を指します。
その為、
「正弦定理」は「sinの定理」（対辺の比率sinを使った公式）、
「余弦定理」は「cosの定理」（底辺の比率cosを使った公式）、
と言われています。
「正弦定理」と「余弦定理」で求める
「三角形」の辺や角度を求める際、
「正弦定理」を使うと、
「１つの辺の長さ」と「２つの角度」から他の「２つの辺の長さ」求める
「２つの辺の長さ」と「１つの角度」から他の「１つの角度」求める
「一つの辺」とそれと向かい合った「１つの角度」から「外接円の半径Ｒ」を求める
のようにして、「三角形」の各値を求める事が出来ます。
おおよそですが、
「得られる角や辺の値の数」と「求めたい角度か辺の値１つ」を合わせた時の総数が
「２辺２角」であれば「正弦定理」を使うと良いです。
つまり、
求める角度、辺を含め「２辺２角」の時は「正弦定理」
「余弦定理」を使うと
「２つの辺の長さ」と「１つの角度」から他の「１つの辺の長さ」を求める
「３つの辺の長さ」から「３つの角度」を求める
のようにして、「三角形」の各値を求める事が出来ます。
おおよそですが、
「得られる角や辺の値の数」と「求めたい角度か辺の値１つ」を合わせた時の総数が
「３辺１角」であれば「余弦定理」を使うと良いです。
つまり、
求める角度、辺を含め「３辺１角」の時は「余弦定理」
極端な話、
「三角形」でさえあれば「正弦定理」か「余弦定理」を使う事で、
・「三角形」の「１つの辺の長さ」が知りたい場合は
他の「１つの辺の長さ」と「２つの角度」
か
他の「２つの辺の長さ」と「１つの角度」
のどちらかの情報が分かれば求める事が可能。
・「三角形」の「１つの角度」が知りたい場合
他の「２つの角度」
か
「３つの辺」
のどちらかの情報が分かれば求める事が可能。
ってだけの事です。
「C# 数学１」で
「直角三角形」のときに使用出来る「辺の比率」や「内角」を求める事が出来る
「三角比」を学びました。
「正弦定理」と「余弦定理」は「(直角でない)三角形」に対しても
「各辺の値」や「内角」を求める事が出来ます。
この後に学ぶ「正弦定理」「余弦定理」の証明の流れを見れば、
結局、「直角三角形の三角比」の定理を使い
「正弦定理」「余弦定理」が成り立っている事が分かると思います。
「正弦定理」計算方法
「正弦定理」を使った計算の方法
「△ABC」があり、
「BC間を辺a」「AC間を辺b」「AB間を辺c」として、
「外接円」の半径を「R」とする。
このとき、
「∠Aの対辺が辺a」
「∠Bの対辺が辺b」
「∠Cの対辺が辺c」
となります。
この時、以下の定理が成り立ちます。
この式を変形すれば、
「１つの辺の長さ」と「２つの角度」から
他の「２つの辺の長さ」を求める事が出来ます。
「正弦定理」を使い、
「辺a」を求める形に式を変形してみます。
この、
「正弦定理」の式を変形した『「辺Ａ」を求める式』から
『各「辺の値」を求める式』を作ると以下の形にまとめる事が出来ます。
「正弦定理」の式を使い、
「sin∠Ａ」を求める形に式を変形してみます。
そこから更に「逆三角関数」を使い、
直接「∠Ａ」を求められるか試してみます。
この、
「正弦定理」の式を変形した『「sin∠Ａ」を求める式』から
『各「sinの角度」を求める式』を作ると以下の形にまとめる事が出来ます。
この「sinの角度」を求める式の形は非常によく使われる為、
「正弦定理」とセットでよく覚えられています。
また、
以下のように式を変形すると
「三角形の外接円の半径Ｒ」を計算する事ができます。
「余弦定理」計算方法
「余弦定理」を使った計算の方法
「余弦定理」には「第一余弦定理」と「第二余弦定理」があります。
「第一余弦定理」は
のような式となりますが、
「第一余弦定理」は現在あまり使われていません。
その為、
最近では「余弦定理」と言った時には暗黙的に
「第二余弦定理」の事を指します。
「第二余弦定理」は
「２つの辺の長さ」と「１つの角度」から
他の「１つの辺の長さ」を求める事が出来ます。
式を変形すれば、
「３つの辺の長さ」から「３つの角度」を求める事が出来ます。
「第二余弦定理」を元に「cos角度」を求める形に式を変形すると以下のようになります。
よって、以下のような式の形となります。
この形は非常によく使われる為、
「第二余弦定理」とセットでよく覚えられているようです。
『「第二余弦定理」の式変形後』の「sin∠Ａ」を求める式から、
「逆三角関数」を使い、直接「∠Ａ」を求められるか試してみます。
「逆三角関数」を使えば「cos∠Ａ」から「∠Ａ」を求める事が可能です。
「正弦定理」「余弦定理」の計算例
ここでは実際に例題を作り、
「正弦定理」と「余弦定理」を使って問題を解いてみます。
「鈍角」「直角」「鋭角」
「三角形」の「１つの角度」は必ず「０°〜180°の間の角度」となります。
「１つの角度」は大きさの範囲により以下のような名前が付けられています。
「正弦定理」「余弦定理」どちらを使うかの判断
この後出てくる例題の「三角形」の「角度」や「辺」を実際に求めるとき、
「正弦定理」と「余弦定理」のどちらを使うか
の判断は概ね以下を基準にして決める事になります。
求める「角度」や「辺」を含めて
「２辺２角」であれば「正弦定理」
「３辺１角」であれば「余弦定理」
が使える事が多いです。
特に注意したいのは「２辺２角」であれば「正弦定理」
「３辺１角」であれば「余弦定理」
が使える事が多いです。
「正弦定理」を使い求めた「sinθ」の値を「角度θ」に変換する時です。
「三角形」の「１つの角度の範囲」は「０°〜180°の範囲内の角度」となります。
これを前提として「sinθ」の値を「角度θ」に変換する際、
「sinθ、角度θ」が「直角」で無い時、
(「sinθ」の値が「１」以外の時、「角度θ」の値が「90°」以外の時)
「角度θ」の値は
「鈍角の角度」と「鋭角の角度」の「２つの角度」を指します。
「２つの角度」のうちどちらの角度かに絞り込みたい場合は、
他の与えられた情報を元に「１つの角度」へと絞り込む
「解の吟味」と言われる工程が必要です。
このような注意が必要なのは、
「正弦定理」で「sinθ」から「角度」を求める
時だけです。
「正弦定理」で「辺」を求める
「余弦定理」で「辺」や「角度」を求める
場合は求めた値がそのまま答えとなります。
(「辺」の値を求めた時の答えは必ず「＋の値」となります)
「cosθ」から「角度」を求めた場合は問題無し。
「例題の準備」
それではまず、例題の為の三角形を準備をします。
ここではこの三角形を使い例題を作り、
各「辺」や各「角度」の答えを求めてみます。
「例題１」(角度を求める)
「∠Ｂ」を求めよ
「２辺２角」なので「正弦定理」を利用して「∠Ｂ」を求めてみます。
「正弦定理」で「sinθ」を求めると「１つの値」となります。
「sinθ」から「角度θ」を求めると殆どの場合「２つの角度の値」となります。
「２つの角度の値」から「１つの角度の値」に絞り込みたい場合は、
他から得られる情報を駆使して「解の吟味」をする必要があります。
(もちろん常に「解の吟味」が可能とは限りませんので、
解が絞り込めない場合は解が複数になる事もあります)
「例題２」(角度を求める)
「∠Ｂ」を求めよ
「３辺１角」なので「余弦定理」を利用して「∠Ｂ」を求めてみます。
「余弦定理」で「cosθ」を求めると「１つの値」となります。
「cosθ」から「角度θ」を求めると「１つの値」となります。
「例題３」(sinＡとcosＡの相互変換)
「三角形」の
「sinＡ」から「cosＡ」を求めたとき
「cosＡ」から「sinＡ」を求めたとき
の違いを以下の例題で確認しておいて下さい。
・例題３−１(sinθからcosθを求める)
「cos∠Ｂ」を求めよ
「三角関数の公式」を使い「cos∠Ｂ」を求めます。
この問題では「cos∠Ｂ」を求めているので「∠Ｂ」は求めません。
・例題３−２(cosθからsinθを求める)
「sin∠Ｂ」を求めよ
「三角関数の公式」を使い「sin∠Ｂ」を求めます。
この問題では「sin∠Ｂ」を求めているので「∠Ｂ」は求めません。
・例題３−３(「三角関数」の公式２の使用)
「cos∠Ａ」を求めよ
「三角関数の公式」を使い「cos∠Ａ」を求めます。
この問題では「cos∠Ａ」を求めているので「∠Ａ」は求めません。
「二重根号(二重ルート)」の解き方は他の章でやる予定ですので、
ここでは解き方が分からなくても大丈夫です。
「cos∠Ｂ」を求めよ
「三角関数の公式」を使い「cos∠Ｂ」を求めます。
この問題では「cos∠Ｂ」を求めているので「∠Ｂ」は求めません。
・例題３−２(cosθからsinθを求める)
「sin∠Ｂ」を求めよ
「三角関数の公式」を使い「sin∠Ｂ」を求めます。
この問題では「sin∠Ｂ」を求めているので「∠Ｂ」は求めません。
・例題３−３(「三角関数」の公式２の使用)
「cos∠Ａ」を求めよ
「三角関数の公式」を使い「cos∠Ａ」を求めます。
この問題では「cos∠Ａ」を求めているので「∠Ａ」は求めません。
「二重根号(二重ルート)」の解き方は他の章でやる予定ですので、
ここでは解き方が分からなくても大丈夫です。
「例題４」(辺を求める)
「辺ｃ」を求めよ
「２辺２角」なので「正弦定理」を利用して「辺ｃ」を求めてみます。
「sin(105°)」を「加法定理」で求める
「sin(105°)」は「sin(60°＋45°)」のように
「計算しやすい角度同士の足し算」で表す事ができます。
これを「加法定理」と言う定理を使い計算すると以下のようになります。
これにより、「sin(105°)」の値を求める事が出来ました。
「三角関数」の中途半端な角度を手作業で求めたい時は、
「加法定理、倍角公式、3倍角公式、半角公式」
などを駆使して値を求める事になります。
ここでは詳しく学びませんが、
「加法定理」の「sin(α＋β)」「sin(α−β)」「cos(α＋β)」「cos(α−β)」
の計算方法位は覚えておいても損は無いです。
但しこれらはあくまで「手計算」で計算を行う際に使用する方法です。
当たり前の事ですが、
結局は「関数電卓」で「三角関数」の角度を求めるのが一番手っ取り早くて簡単です。
ここから先は、
「正弦定理」と「余弦定理」の証明を
出来るだけ図を使い説明してみます。
「円周角の定理」(外角の定理)と「四角形の外接円」
「正弦定理」の証明を学ぶ前に
「円周角の定理」と「外角の定理」と「四角形の外接円」について知る必要があります。
「円周角」と「中心角」とは
「円周角」と「中心角」とは以下の部分の事を指します
「円周角の定理」
「円周角」と「中心角」は常に以下のような関係にあります。
このため、
「直径」の線を辺として三角形を作ると、
必ず「円周角」が「90°」の「直角三角形」となります。
「円周角の定理」の証明(外角の定理)
「円周角の定理」の証明を行います。
まずは三角形の「外角の定理」を知っておく必要があります。
・三角形の「外角の定理」
それでは、
「円周角の定理」の証明を行います。
・「円周角の定理」の証明、その１
・「円周角の定理」の証明、その２
・「円周角の定理」の証明、その３
・「円周角の定理」の証明、その４
正円上の「円周角と中心角」の全ての場合分けとなる
上記『「円周角の定理」の証明、その１〜３』により
常に「円周角の２倍が中心角」と言えます。
つまり、
正円の
「中心角」が１つの角度であるとき、
「円周角」の角度はどの位置にあっても常に「同じ角度」を保つ
ことが分かります。
「円周角の定理の逆」
この「円周角の定理の逆」を使用すれば、
以下のようにして四角形の各角度を求める事が出できます。
「四角形の外接円」
「四角形の外接円の性質」の証明は以下の通りです。
「正弦定理」の証明
三角形の角度の種類（鋭角、直角、鈍角）
三角形の角度には「鋭角、直角、鈍角」の３種類が存在します。
「∠Ａ」の角度が「鋭角」か「直角」か「鈍角」かによって、
「正弦定理」の証明方法が変わります。
「正弦定理」の覚え方
・「正弦定理」を覚える
上記公式の角度と辺の関係は以下のイメージで覚えておくと良さそうです。
・「辺」を求める形を覚える（正弦定理）
「正弦定理」の公式から「辺ａ」を知る為に、
「辺ａの値」を求める式に変形すると以下の式となります。
（式の変形方法は前述『「正弦定理」計算方法』に記述してあります）
この『「正弦定理」の式変形後』の式は無理に覚える必要はなく、
毎回「正弦定理」の公式から式を変形して導き出した方が早いです。
一応この式をイメージで表すと以下のような感じになります。
・「角度」を求める形を覚える（正弦定理）
「正弦定理」の公式から「sin∠Ａ」を知る為に、
「sinの角度」を求める式に変形すると以下の式となります。
（式の変形方法は前述『「正弦定理」計算方法』に記述してあります）
この『「正弦定理」の式変形後』の式は無理に覚える必要はなく、
毎回「正弦定理」の公式から式を変形して導き出した方が早いです。
一応この式をイメージで表すと以下のような感じになります。
「正弦定理」は「sin」を使用した定理の事です。
（対辺の比率sinを使用した定理。「正弦」の事を「sin」と呼びます）
それでは、
「正弦定理」の証明を
「鋭角」「直角」「鈍角」それぞれの状況で行います。
「鋭角(∠Ａ＜90°)」三角形の「正弦定理」の証明
「正弦定理」の証明
この「辺ａ＝sin∠Ａ＊２Ｒ」の式を利用して、
よって上図により、三角形の一つの角が「鋭角」であるときこの「辺ａ＝sin∠Ａ＊２Ｒ」の式を利用して、
「正弦定理」の公式と同じ式となる事が分かります。
「直角(∠Ａ＝90°)」三角形の「正弦定理」の証明
「正弦定理」の証明
この「辺ａ＝sin∠Ａ＊２Ｒ」の式を利用して、
よって上図により、三角形の一つの角が「直角」であるときこの「辺ａ＝sin∠Ａ＊２Ｒ」の式を利用して、
「正弦定理」の公式と同じ式となる事が分かります。
「鈍角(∠Ａ＞90°)」三角形の「正弦定理」の証明
「正弦定理」の証明
この「辺ａ＝sin∠Ａ＊２Ｒ」の式を利用して、
よって上図により、三角形の一つの角が「鈍角」であるときこの「辺ａ＝sin∠Ａ＊２Ｒ」の式を利用して、
「正弦定理」の公式と同じ式となる事が分かります。
「余弦定理」の証明に必要な知識
これから行う「余弦定理の証明」に必要となる知識を
ざっと羅列しておきます。
「三角比の各辺の値の求め方」「180°−θ公式」
これは、前回「C# 数学１」で学んだ内容ですね、
（「三角比の角辺の値の求め方」は「正弦定理の証明」でも出てきました）
「余弦定理」の証明では、以下のような形で頻繁に使用されますので、
しっかりと覚えておいて下さい。
「(三平方)ピタゴラスの定理」
これも、前回「C# 数学１」で学んだ内容ですね
「三角関数」の公式２
これも、前回「C# 数学１」で学んだ内容です。
「sinθ」か「cosθ」のどちらかの値が分かれば
もう一つの値も分かるという公式です。
「第二余弦定理」の証明
三角形の角度の種類（鋭角、直角、鈍角）
三角形の角度には「鋭角、直角、鈍角」の３種類が存在します。
「∠Ａ」の角度が「鋭角」か「直角」か「鈍角」かによって、
「第二余弦定理」の証明方法が変わります。
「第二余弦定理」の覚え方
・「第二余弦定理」を覚える
上記公式の式は以下のイメージで覚えておくと良さそうです。
「辺ａ」以外の「辺ｂ」「辺ｃ」を求める式でも
同じ手順で式を作る事ができます。
・「角度」を求める形を覚える（余弦定理）
「第二余弦定理」の公式から「cos∠Ａ」などの
「cosの角度」を求める形に式を変形すると以下ような式となります。
（式の変形方法は前述『「余弦定理」計算方法』に記述してあります）
上記全ての辺から角度を求める式は以下のイメージで覚えておくと良さそうです。
「cos∠Ａ」以外の「cos∠Ｂ」「cos∠Ｃ」を求める式でも
同じ手順で式を作る事ができます。
「余弦定理」は「cos」を使用した定理の事です。
（底辺の比率cosを使用した定理。「余弦」の事を「cos」と呼びます）
それでは、
「第二余弦定理」の証明を
「鋭角」「直角」「鈍角」それぞれの状況で行います。
「鋭角(∠Ａ＜90°)」三角形の「第二余弦定理」の証明
「第二余弦定理」の証明
この「ａ２＝(ｃ−ｂ＊cos∠Ａ)２＋(ｂ＊sin∠Ａ)２」の式を利用して、
同様に
「ｂ２＝ ｃ２＋ａ２−２ｃａ＊cos∠Ｂ」
「ｃ２＝ ａ２＋ｂ２−２ａｂ＊cos∠Ｃ」
も成り立ちます。
よって上図により、三角形の一つの角が「鋭角」であるときこの「ａ２＝(ｃ−ｂ＊cos∠Ａ)２＋(ｂ＊sin∠Ａ)２」の式を利用して、
同様に
「ｂ２＝ ｃ２＋ａ２−２ｃａ＊cos∠Ｂ」
「ｃ２＝ ａ２＋ｂ２−２ａｂ＊cos∠Ｃ」
も成り立ちます。
「余弦定理」の公式と同じ式となる事が分かります。
では、以下のような「鋭角」の三角形の時はどう証明すれば良いのでしょうか？
これは、以下のように考えれば解決できます。
これで証明できるのですが、
もう少し向き合った証明の仕方も試してみます。
「第二余弦定理」の証明
この「ａ２＝(ｂ＊cos∠Ａ−ｃ)２＋(ｂ＊sin∠Ａ)２」の式を利用して、
同様に
「ｂ２＝ ｃ２＋ａ２−２ｃａ＊cos∠Ｂ」
「ｃ２＝ ａ２＋ｂ２−２ａｂ＊cos∠Ｃ」
も成り立ちます。
よって上図により、三角形の一つの角が「鋭角」であるときこの「ａ２＝(ｂ＊cos∠Ａ−ｃ)２＋(ｂ＊sin∠Ａ)２」の式を利用して、
同様に
「ｂ２＝ ｃ２＋ａ２−２ｃａ＊cos∠Ｂ」
「ｃ２＝ ａ２＋ｂ２−２ａｂ＊cos∠Ｃ」
も成り立ちます。
「余弦定理」の公式と同じ式となる事が分かります。
「直角(∠Ａ＝90°)」三角形の「第二余弦定理」の証明
「第二余弦定理」の証明
同様に
「ｂ２＝ ｃ２＋ａ２−２ｃａ＊cos∠Ｂ」
「ｃ２＝ ａ２＋ｂ２−２ａｂ＊cos∠Ｃ」
も成り立ちます。
よって上図により、三角形の一つの角が「直角」であるとき同様に
「ｂ２＝ ｃ２＋ａ２−２ｃａ＊cos∠Ｂ」
「ｃ２＝ ａ２＋ｂ２−２ａｂ＊cos∠Ｃ」
も成り立ちます。
「余弦定理」の公式と同じ式となる事がわかります。
「鈍角(∠Ａ＞90°)」三角形の「余弦定理」の証明
「第二余弦定理」の証明
この「ａ２＝(ｃ−ｂ＊cos∠Ａ)２＋(ｂ＊sin∠Ａ)２」の式を利用して、
同様に
「ｂ２＝ ｃ２＋ａ２−２ｃａ＊cos∠Ｂ」
「ｃ２＝ ａ２＋ｂ２−２ａｂ＊cos∠Ｃ」
も成り立ちます。
よって上図により、三角形の一つの角が「鈍角」であるときこの「ａ２＝(ｃ−ｂ＊cos∠Ａ)２＋(ｂ＊sin∠Ａ)２」の式を利用して、
同様に
「ｂ２＝ ｃ２＋ａ２−２ｃａ＊cos∠Ｂ」
「ｃ２＝ ａ２＋ｂ２−２ａｂ＊cos∠Ｃ」
も成り立ちます。
「余弦定理」の公式と同じ式となることが分かります。
「第一余弦定理」の証明
証明の為の三角形の形２パターン
三角形の「底辺」に対して「頂点∠Ａ」がどの位置にあるかによって
「第一余弦定理」の証明方法が変わります。
「第一余弦定理」のおさらい
通常「余弦定理」と言った場合「第二余弦定理」の事を指します。
「第一余弦定理」の方の定理は使われる事が少ないです。
「頂点が底辺の範囲内」のときの「第一余弦定理」の証明
「第一余弦定理」の証明
同様に
「辺ｂ＝ 辺ｃ＊cos∠Ａ ＋ 辺ａ＊cos∠Ｃ」
「辺ｃ＝ 辺ａ＊cos∠Ｂ ＋ 辺ｂ＊cos∠Ａ」
も成り立ちます。
よって上図により、「頂点が底辺の範囲内」のとき同様に
「辺ｂ＝ 辺ｃ＊cos∠Ａ ＋ 辺ａ＊cos∠Ｃ」
「辺ｃ＝ 辺ａ＊cos∠Ｂ ＋ 辺ｂ＊cos∠Ａ」
も成り立ちます。
「第一余弦定理」の公式と同じ式となる事が分かります。
「頂点が底辺の範囲外」のときの「第一余弦定理」の証明
「第一余弦定理」の証明
同様に
「辺ｂ＝ 辺ｃ＊cos∠Ａ ＋ 辺ａ＊cos∠Ｃ」
「辺ｃ＝ 辺ａ＊cos∠Ｂ ＋ 辺ｂ＊cos∠Ａ」
も成り立ちます。
よって上図により、「頂点が底辺の範囲内」のとき同様に
「辺ｂ＝ 辺ｃ＊cos∠Ａ ＋ 辺ａ＊cos∠Ｃ」
「辺ｃ＝ 辺ａ＊cos∠Ｂ ＋ 辺ｂ＊cos∠Ａ」
も成り立ちます。
「第一余弦定理」の公式と同じ式となる事が分かります。
まとめ「正弦定理」「余弦定理」
「正弦定理」と「外接円の半径を求める形」
「正弦定理」の式変形（辺を求める形）
「正弦定理」の式変形（sin角度を求める形）
「第一余弦定理」(あまり使われません)
「第二余弦定理」（辺を求める）
「第二余弦定理」の式変形（cos角度を求める形）
C# 統計･微分積分･線形代数への道
次へ→http://1studying.blogspot.jp/2017/08/senkei-index.html#kuw03
他
以下のサイトを参考にしました。
正弦定理とは何か？2つの視点から分かる公式の覚え方・考え方
http://atarimae.biz/archives/18398
正弦定理を使った練習問題一覧
http://manapedia.jp/text/2916?page=3
正弦定理と余弦定理の違いと使い方
http://www24.atpages.jp/venvenkazuya/mathA/Agraphic6.php
正弦定理とは？公式や余弦定理との使い分けをわかりやすく解説！
https://www.studyplus.jp/353
【図形と計量】正弦定理と余弦定理のどっちを使えばいいんですか？
https://kou.benesse.co.jp/nigate/math/a13m0316.html
5分でわかる！正弦定理と余弦定理の使い分け
https://www.try-it.jp/chapters-6150/sections-6229/lessons-6250/
0 件のコメント:
コメントを投稿